Heat Capacity Worksheet - Answer Key

 

Back to the other Thermodynamics Workbooks and other General Chemistry Workbooks

Go To -> Worksheet - Answer Key - Solutions Manual

  1. What is molar heat capacity? 

    The energy required to raise the temperature of 1 mol of a substance by 1K.  Represented by, C.

    2.  

     

  2. What is specific heat capacity?

    The energy required to raise the temperature of 1 gram of a substance by 1K.  Represented by, C.

    3.  

     

  3. The kinetic energy of a system is directly related to its temperature.  So if we heat a system we increase its kinetic energy.

    4.  

     

  4. What are two conditions under which a gas can be heated?

      5.  

    • Constant Volume. 

      •  

    • Constant Pressure. 

     

     

  5. What are the values for:

      6.  

    • Cv = 3/2 R

      •  

    • Cp = Cv + R = 5/2 R

     

     

  6. Why is Cv<Cp?

    Cp > Cv because energy gets used for heating and work in constant pressure situation. 

    7.  

     

  7. When energy is added to a molecule there are three potential forms of motion that it can be transferred into:

      8.  

    • Translational – The molecule’s movement around the container
                                                                                                     
    • Vibrational – The spring-like movement of the bond between atoms.

      •  

    • Rotational – The spinning of the molecule on an axis.

     

     

  8. Translational motion is the only motion that directly affects temperature.

    9.  

     

  9. The values 3/2 R and 5/2 R are only applicable to monatomic ideal gases. Why?

    A monatomic ideal gas is only capable of undergoing translational motion.

    10.  

     

  10. This means that the calculated molar heat capacities are often less than actual molar heat capacities.

    11.  

     

  11. What equation relates ΔE to heat capacity? 

    ΔE = nCVΔT

      12.  

    • Under what conditions can you use this equation?

      Under any all conditions. 

      •  

    • Under what conditions does ΔE = q?

      When the volume is constant.

     

     

  12. What equation relates ΔH to heat capacity?

    ΔH = nCpΔT

      13.  

    • Under what conditions can you use this equation?

      Under any all conditions. 

      •  

    • Under what conditions does ΔH=q?

      When the pressure is constant.

     

     

  13. Which value of R do we use in these equations?

    R = 8.3145 J mol-1K-1

    14.  

     

  14. Fill in the chart.

                 

     

     

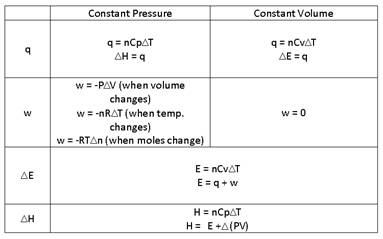
  1. Consider a sample containing 5 moles of a monatomic ideal gas that is taken from State Aà State B by 2 different paths.  For each step, assume that the external P is constant and equals the final P of the gas for that step.  Calculate the values of q, w, ΔH and ΔE for each step along the 2 paths and the totals for the 2 paths.  What do the totals demonstrate?

    Path A:             q = 2.3 kJ                                 Path B:             q = 14.4 kJ
    w = 9.1 kJ                                                        w = – 3.04 kJ
    ΔE = 11.4 kJ                                                     ΔE = 11.4 kJ
    ΔH = 19.0 kJ                                                    ΔH = 19.0 kJ
                       

    The values of q and w are path dependent. 

     

    The values of ∆H and ∆E are path independent.

Home . Support Us . Contact Us